蜂鸟e203集成，单通道加法器

流水线

执行模块

执行模块包含定点寄存器堆（Integer Regfile）、浮点寄存器堆（Floating Point Regfile）、操作数选择模块（Opcode Sel）、定点运算单元（Alu）、浮点运算单元（FPU）以及一个访存单元（Mem Unit）。

译码模块对指令译码之后得到对应的 OP 等操作信息以及源操作数地址，执行模块根据源操作数地址首先从定点和浮点寄存器堆中取出对应的操作数，然后操作数选择模块从寄存器堆输出结果以及旁路数据中选择正确的操作数，最后运算单元根据相应操作信息及其操作数就可以计算出结果。

对于定点指令来说，最多需要从定点寄存器堆中取出两个源操作数，而对于浮点指令来说，最多需要从浮点寄存器堆中取出三个源操作数。定点寄存器堆必须具有 2 个读端口，而浮点寄存器堆必须具有 3 个读端口。同样为了确保写回阶段每次能够写回操作数，2 个寄存器堆都必须具有一个写端口。

FPU

具有六条独立的流水线。各运算单元的输入为三个操作数（OP1、OP2、OP3）和舍入模式（Roud_mode），各单元运算完成后，将输出运算结果以及五种异常。

浮点加/减法器

加法器接收三个输入：两个操作数（OP1、OP2），三位舍入模式；输出四个异常信号，即上溢、下溢、无效和不精确。

主要功能单元分为预处理单元、二进制加减单元和后处理单元三部分。

预处理阶段将输入操作数分解为符号位、尾数位和指数位。

浮点乘法器

• 符号位异或
• 指数位相加
• 尾数位相乘
• 最后根据浮点数格式对得到的指数位和尾数位进行调整，并进行舍入处理

前导 0 预测，比较、转换指令

前导0预测

• 操作数关系编码

  

• 前导 0 预测预测逻辑

  

• 由此根据公式可以不断推算前导零的存在[30]，在计算过程中会同时计算尾数A-B 和 B-A 的结果，这是因为在阶码相等时，无法判断哪个操作数较大。浮点运算设计中，保持以大数减小数的设计，需要出判断较大的操作数，为了节省整体计算时间，同时计算两者的结果，在判断出较大的操作数之后，最后根据操作数大小进行结果选择。

乘法

（？）浮点尾数计算的区别在于，尾数表示的是结果的小数部分，所以每一位对应的权重是负数，所以每一个部分积结果对应的是右移，需要从高位到低位进行计算。

比较、转换

比较

对于减法和比较指令的设计，都是可以正常兼容与浮点加法中，比如减法就可以转换为符号异位的加法操作，只需要考虑符号位和减法操作的匹配情况。对于比较指令同样是可以在加法计算中通过复用数据通路直接获得结果。在浮点加法模块中可以兼容 fmin、fmax、fle、flt、feq 这五条比较指令在各精度下的计算。

转换

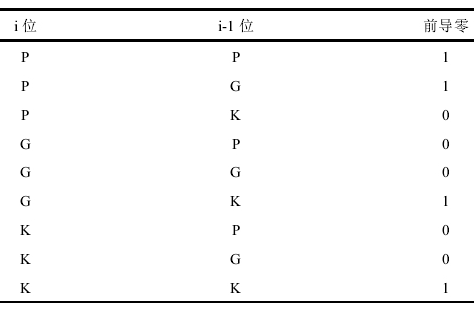
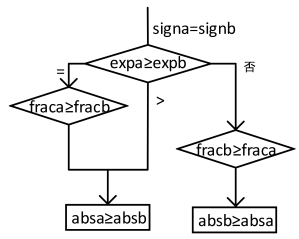
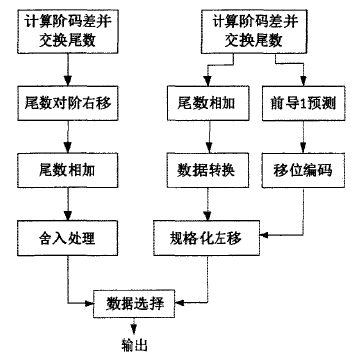
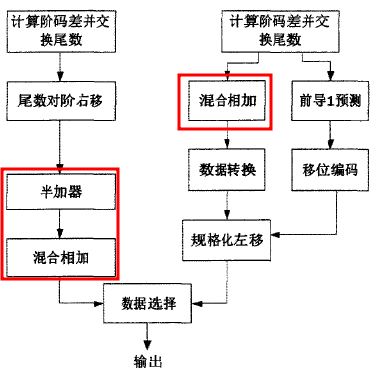
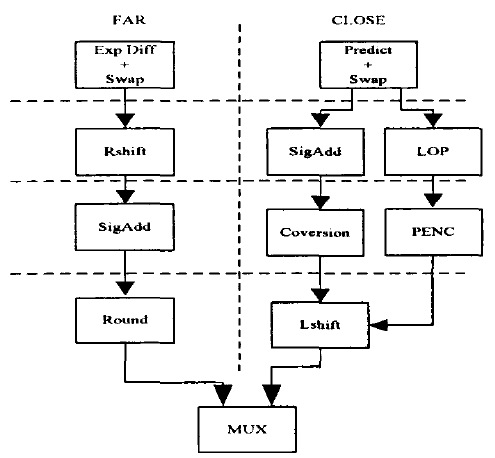
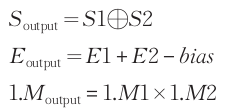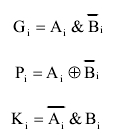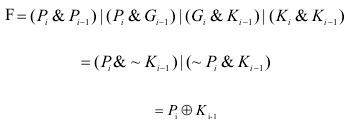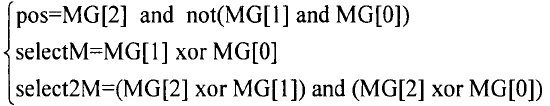双路径，四级、三级，前导0检测（非预测，优先权、二分），booth补码乘法，舍入

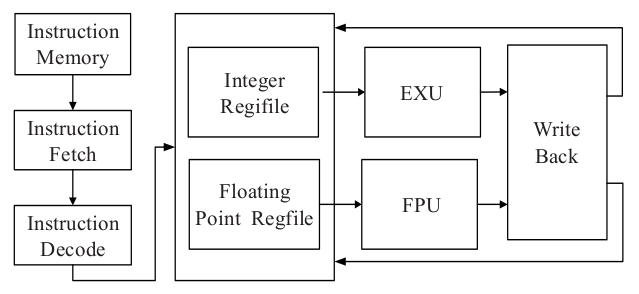
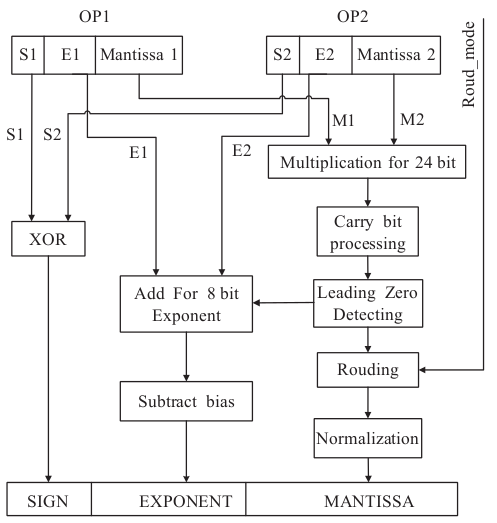
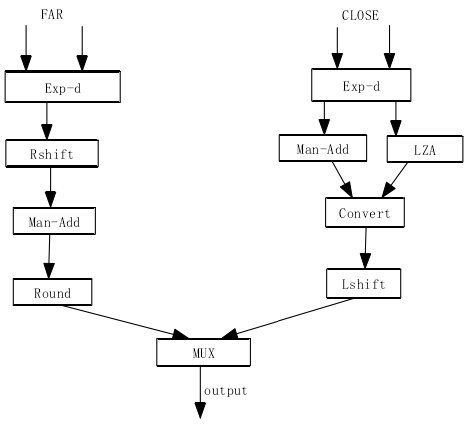
加法器结构

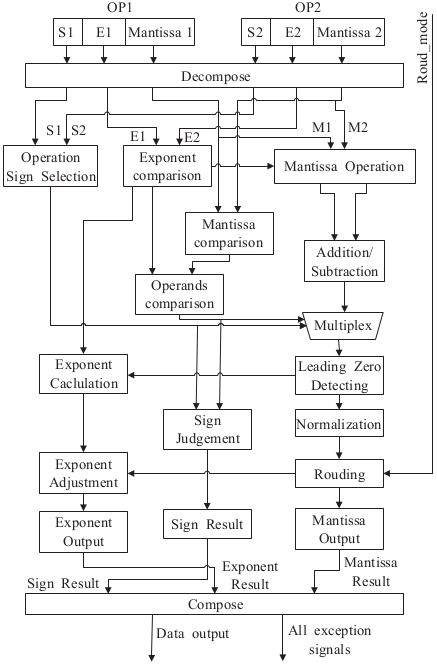
two - path

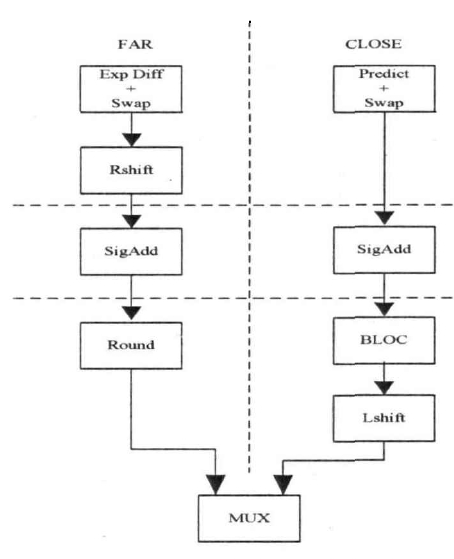
通路和通路当阶码差值小于等于1时，尾数运算结果规格化移位所需的时间比较长，而对阶移位所需时间比较短，称为CLOSE通路。
而当阶码相差大于1时，则结果规格化移位所需时间比较短，而对阶移位所需时间比较长，称为FAR通路。

前导 0 预测

在对阶移位和规格化移位中，对阶移位的移位数直接由两个操作数的指数差值决定，而规格化移位的移位数必须通过对结果尾数进行检测才可以得到。
因此，规格化移位中的前导零的检测直接影响着浮点加法部件的性能。

针对前导零检测，人们运用部分压缩和重编码理论进行了前导零预判。在进行尾数加减操作的同时对操作数进行部分压缩和重编码从而预测结果尾数的前导零
个数。但是前导零预判技术硬件代价较大，电路逻辑复杂，所以在运用此技术的同时要考虑面积和功耗的因素。

在传统的方法中，规格化操作是在得到尾数加减的非规格化结果后进行的，这样做可以使实现方法变得简单。但是这种方法也存在一个问题，即增加了浮点运算的关键路径长度，加大了单元的延迟时间。

优先权判断

直接对结果从高位到低位进行一位一位的检测并记数，直到检测到最高位的为止。这种方法实现简单、直观。但是它存在延迟大，电路扇入扇出大，逻辑复杂的缺陷。

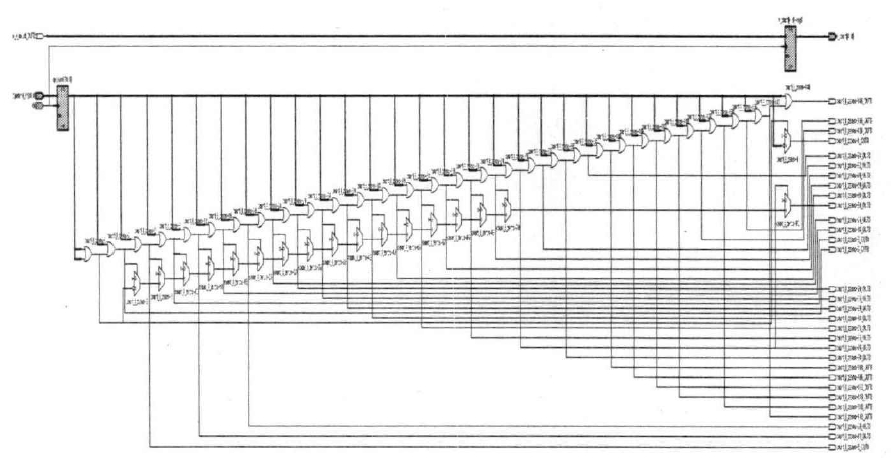
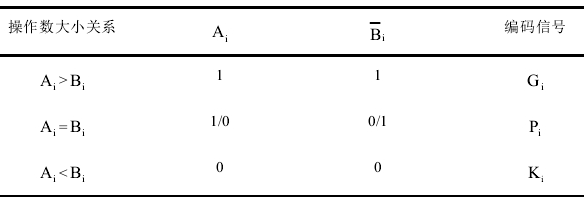
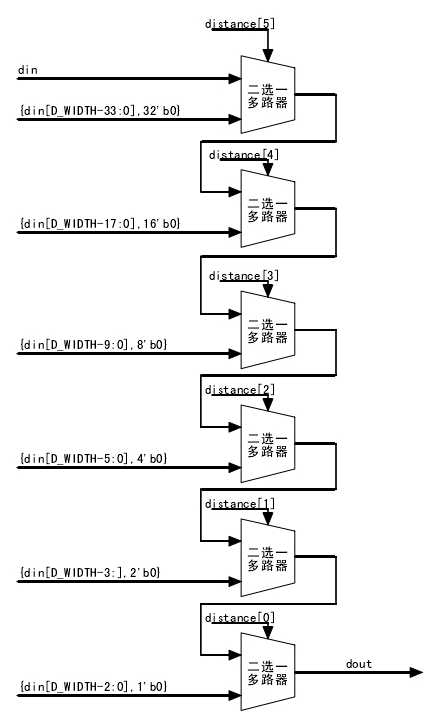
二分检测法

如果输入二进制串的左半子串是全零串，那么检测结果的最高有效位为，检测结果的剩余部分就是右半子串的检测结果。否则，检测结果的最高有效位为‚检测结果的剩余部分就是左半子串的检测结果。这个结论可以递归地应用于两个更小的子串。

二分检测法将大的二进制串分解成小的子串，各个子串的前导零检测同时进行，最后进行逻辑组合得到最终的前导零个数，解决了优先权编码检测器的大扇入扇出问题，简化了电路逻辑，优化了电路结构，并且更重要的是大大的提高了电路的工作速度。

尾数分割成的子串数越多，每个子串前导零检测时间越少，但是需要的加法器以及选择器就越多，各个子串的前导零数相加的时间就越大。为此要综合平衡子串个数以及由此产生的级数。

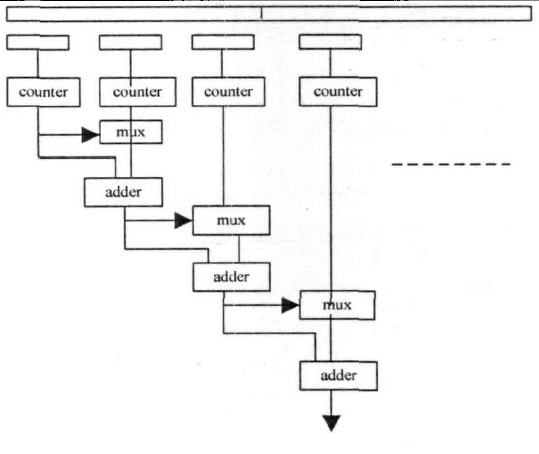
文中例子，划分为2个子串频率最高，划分为4个、8个则频率逐渐降低。

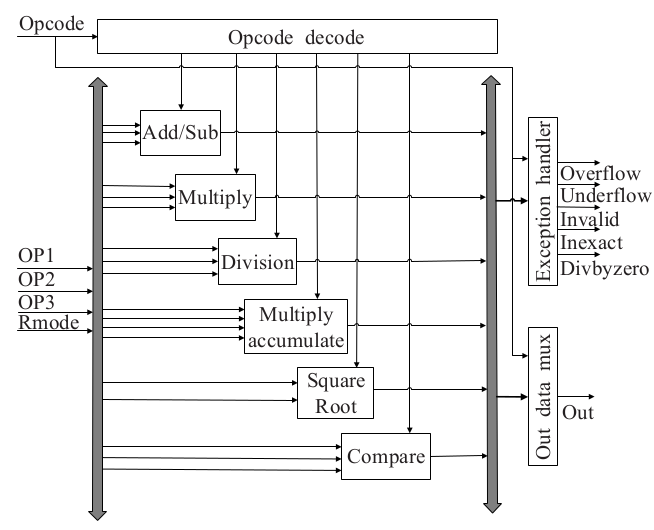
加法器结构设计

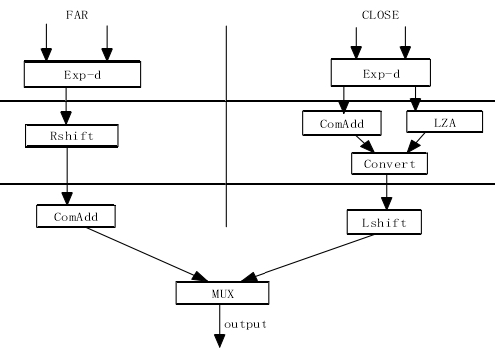
如果采用流水技术，一个浮点加法器可分成四级流水，完成一个浮点加法运算需要一个周期。但是在本文设计的中‚为了使的控制逻辑简单，保证操作顺序输入结果顺序输出，使浮点加法与乘法的三段流水一致，所以本文在一算法加法器的结构上对之进行结构改进。

在本文的设计中，将FAR通路中的耗时较少的操作数交换和尾数右移合二为一，在一个时钟周期内完成，对于CLOSE通路运用前导零的二分检测法可以将结果规格化和左移在一个时钟周内完成。

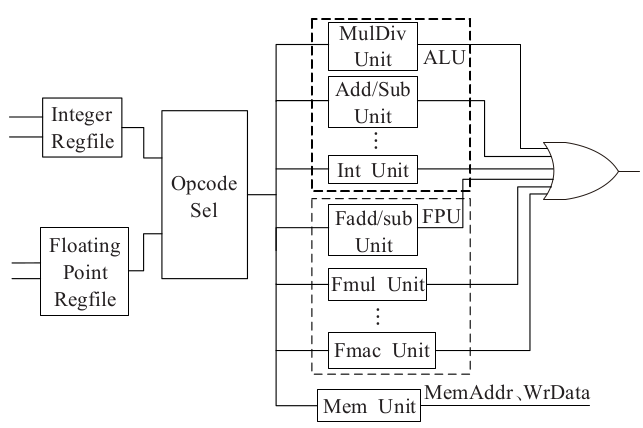
乘法器

乘法流程

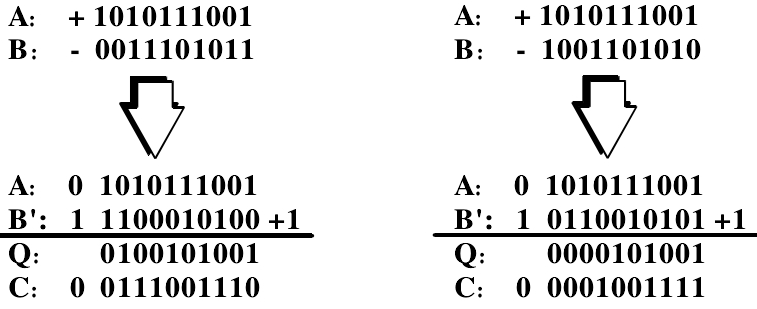
1. 检测操作数是否为0，并设置结果数：如果操作数中有一个为 0 ，乘积必为 0 ，不必做其他操作；如果均不为0，方进行乘法运算。结果数符号按同号相乘为正，异号相乘为负的规则确定。
2. 阶码相加。阶码相加可能产生溢出，应当注意。同号相加可能上溢，也可能下溢。此时要检测溢出异常，使得处理单元转入溢出处理。
3. 尾数相乘。这可以用任何一种定点小数乘法实现
4. 乘法规格化。尾数相乘后，可能需要右规。由于尾数是定点小数（非规格数？），相乘后不会出现需要左规的情况。右规是阶码加，有上溢的可能。

Booth

算法的基本思想如下乘数被划分为一系列三位子串，每个子串分别与相邻的子串有一位重叠，而第一个子串是由乘数的最低两位和组成。编码器则根据这些子串的内容产生编码以指导部分积的生成。

用三个控制位来表达这些信息。其中 selectM 为 1 表示部分积的绝对值是被乘数绝对值的 1 倍， select2M 为 1 为表示部分积的绝对值是被乘数绝对值的 2 倍，pos 为 0 表示部分积的符号与被乘数的相同，为 1 则表示部分积的符号与被乘数的相反。

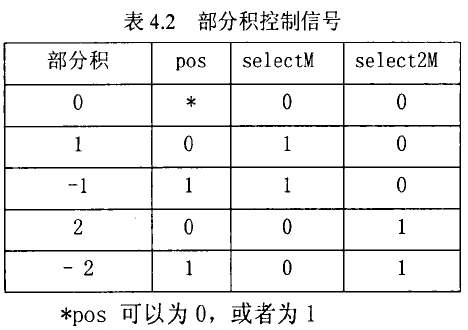
控制逻辑：可以看出，selectM 和 select2M 需要两个门延迟就能得到，而 pos 需要 3 个门延迟，是关键路径。同时，此关键路径的实现需要两个与门和一个反向器，面积开销较大。

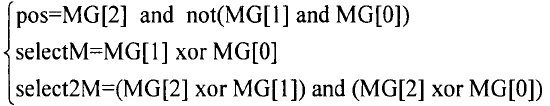
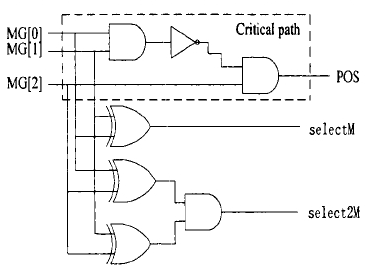
通过伪 1 变换减少 BOOTH 算法延迟

当部分积为 0 （MG = 000 | 111）时，pos 可为 1 也可为 0 。直接用 MG[2] 表示 pos （定义为pos2），可以看出仅当 MG 为 111 时 pos2 != pos1 ，但此时部分积 为 0 ，并不产生影响。

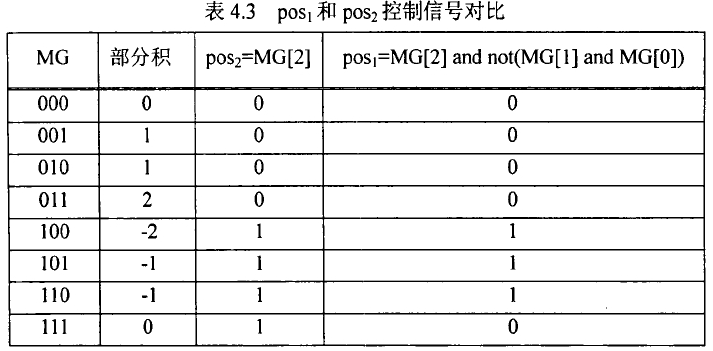
所以可以直接用直接用 MG[2] 表示 pos ，简化逻辑：

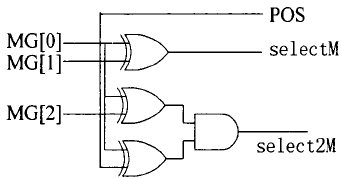
舍入

• 就近舍入 RNE/RMM ：舍入为最近可表示的数

  多余位的值超出规定的最低有效位值 LSB 的一半，则应向最低有效位进 1，否则简单的截尾即可。对于恰好是的一半值的这种特殊情况，要根据当前的值来分别讨论若 LSB 现为 0 ，则简单的截尾；若 LSB 现为 1 ，则向 LSB 进1。

• 朝 0 方向舍入 RTZ：截取所需位数，舍弃后面所有位

  简单地截尾。

• 朝 $-\infty$ 舍入 RDN ：总是取左边最近可表示数

  对正数来说，直接截尾。

  对负数来说，多余位全为 0 则直接截尾，不全为 0 则向 LSB 进 1。

• 朝 $+\infty$ 舍入 RUP ：总是取右边最近可表示数

  对正数来说，多余位全为 0 则直接截尾，不全为 0 则向 LSB 进 1 。

  对负数来说，直接截尾。

双路径，五级、三级，前导0预测，桶形移位器

双路径

经过上面分析，双路径算法就应运而生了，M.J. Flynn 等人, 提出了双路径算法(Michael.J.Flynn,1990):

它的基本思想是根据两操作数的指数差异大小来划分数据通路。这是因为，当指数差异较小时，两指数进行减法操作时．其结果将可能产生大量的前导零，这在规格化的时候将产生大量的左移操作，而移位的位数是个变量：当指数差异较大时，又将在对齐指数时产生大量的移位。浮点加法器的双数据通道划分方法在浮点加法器的结构设计中被广泛采用。

通过对 CLOSE 路径和 FAR 路径这 2 条路径分析，发现双路径算法相对于传统的加法算法的改进主要在于，在每条路径中，只有一次全长的移位。

FAR路径中，要么进行加法运算，要么进行指数差异较大的减法运算，所以

• 最终的尾数在规格化时候，不需要移位或者只需要进行一位左移

• 尾数运算结果始终为正．不需要转换成原码的转换操作。

• A跟B的指数相差非常大，则相当于对1个无穷大数进行不痛不痒的加减操作，这样的话，可以将较大的数（即A）当成结果直接输出。

CLOSE路径中，由于A跟B指数差d<=1．所以

• 对齐操作的移位，最多为1位

• d的计算只由最后两位相减

• 舍入可以避免。

五级

• Exp-d： 求指数之差同时交换 2 个操作数 A,B，总是让大操作数用 A 表示，小操作数用 B 表示。
• Rshift: B 右移向 A 对齐,移动的位数由 Exp-d 中计算出来的指数之差 d决定。
• Man-Add: 尾数有效位相加减（减法也是通过加法实现)。
• Round： 舍入操作。
• LZA: 前导 0 判断，主要应用在指数相差不大的减法操作中。
• Convert: 减法可能出现负数，这样需要进行负数转原码表示的转换。
• Lshift: 根据前导零的结果，判断第一个 1 出现的位置，从而进行左移，使尾数符合标准 IEEE754 表示的标准。

三级

为了进一步优化, Flynn 等人继续做出改进,提出了合并舍入的方法,在有效位加法器的设计上进行改进,针对 IEEE 四种舍入方式的计算要求,用结合了 CLA 跟CSA2 种加法器优点的混和加法器 ComAdd 完成所有舍入可能结果的计算, 这种改进将原来五周期的传统浮点加法算法缩短为三周期完成。

• Exp-d： 求指数之差同时交换 2 个操作数 A,B，总是让大操作数用 A 表示，小操作数用 B 表示。
• Rshift: B 右移向 A 对齐,移动的位数由 Exp-d 中计算出来的指数之差 d决定。
• ComAdd： 复合加法器，可以将舍入合并在尾数有效位加法器中。
• LZA: 前导 0 判断，主要应用在指数相差不大的减法操作中。
• Convert: 减法可能出现负数，这样需要进行负数转原码表示的转换。
• Lshift: 根据前导零的结果，判断第一个 1 出现的位置，从而进行左移，使尾数符合标准 IEEE754 表示的标准。

运算部件

错位并行指数比较、尾数移位

sd

尾数有效位加法器

减法

sfa

前导 0 预测

前导 0 预测仅在CLOSE路径进行。

加法运算：不需要前导 0 预测

减法运算：

• 始终采取大数减小数 A - B

• 

• 如果是采用大操作数减去小操作数的话，Q(采用公式预测的结果)跟 C（实际算出来的结果），Q 跟 C 要么相同，要么差了一位（多计算一个前导零），而这个差一位的情况可以在后面进行微调，如果不微调，则会在左移过程中将首个 1 移走。

• 这个前导零预测电路有个局限性，只有当是大操作数减去小操作数时候才有用，而如果是小操作数减去大操作数，就会出现预测错误。而我们知道，前导零预测电路主要应用在 CLOSE 路径中，尽管我们之前会根据指数大小来判断操作数大小，但是如果指数相同的情况下，我们并没有采用再对具体尾数比较来判断大小，因为这样会加深电路结构的复杂化，且降低速度，而是任由 2 操作数哪个减去哪个，所以这里，并行的思想再次得到体现，我们分别用两个前导零预测（？）电路，一个预测（A-B）的前导零计数，一个预测（B-A）的前导零计数，然后由最终结果来选择准确的需要移位的数目的。

桶形移位器

桶形移位器(Barrel Shifter)是微处理器定点/浮点运算器中的典型运算部件。桶形移位器的基本构成使多路复用器,设计如果使采用标准单元综合的话，它所占用的面积较大，如果设计对时序，面积有很高要求的话，则不适合。所以我们可以采用自己设计的桶形移位器(Rafati, R.Fakhraie, S.M Smith, K.C.,2006)，可以避免标准单元综合的桶形移位器在时序，面积上面的缺点，当在需要多次重复使用以及要求速度的设计中，能得到广泛的使用，因此在High-performance跟Low power的微CPU的设计中,通常都采用全定制设计的桶形移位器来实现移位功能。

舍入

two - path

• 结论1

  如果将两个正规化的浮点数完成加法运算，则规格化的结果最多只需要向右移一位。

• 结论2

  如果两数 $|\Delta E| > 1$ ，那么规格化的减法运算结果仅需要向左移动一位。

Farmwald 经过对浮点加法运算的算法进行了分析与研宄，对浮点加法算法进行了一系列的改进。

• 在传统浮点加法的算法中，在两个尾数完成相减时，其结果可能为负值，此时需要通过数据转换操作来将减数和被减数进行交换来避免运算结果为负值的情况。

  如果两浮点数的阶码大小相等，两尾数相减的结果仍然可能为负值，因此还需要将数据进行转换。这种情况下，不需要对运算结果进行舍入处理。因为在两尾数交换的算法中，数据转换与舍入操作是处于相互排斥的，此时将其操作的加法器进行合并来减少一部分加法运算的执行时间。

• 在完成两个浮点数的尾数加法运算时，可能存在进位的情况，使得尾数完成运算后得到的结果的位数会增加１位，此时必须使用一个全长度的对阶移位器。

  对于减法运算，可分两种情况讨论：当两浮点数的阶码差值 $|\Delta E| > 1$ 时，对于这种情况需要一个全长度的指数对阶移位器，对于运算结果的规格化处理时，仅需要将结果向左移动一位，把该路径记为；当两浮点数的阶码差值 $|\Delta E| \leq 1$ 时，在对尾数的运算结果进行规格化处理需要一个全长度的移位器，而不需要全长度的对阶移位器，把该路径记为CLOSE路径。根据上述可知浮点数的指数对阶移位器与尾数规格化处理移位器是互斥的。因此在FAR路径和CLOSE路径中仅仅需要一个全长度的移位器即可，这可进一步减少了加法运算的时间。

• 在进行规格化处理尾数运算的结果时，采用前导１预测算法判定移位的位数。前导１检测算法是对运算的结果进行检测前导０的数目，而前导１预测算法是将两个尾数作为输入来预测运算结果的前导０的数目。这一改进使得尾数运算操作的并行度增加，提高运算速度，又进一步的降低了算法的执行时间。

合并舍入 two - path

在1990年Quach与Flynn共同提出了根据 two - path 算法的研宄而进行改进得来的一种新型的浮点加法运算的算法。

• Quach对 two - path 算法的舍入处理操作进行了优化，使得 two - path 减少了加法运算的一部分操作。同时他还提出了利用预先就算出所有可能存在的结果，然后再对结果进行选择而得到正确的值。这样可以减少舍入处理和补码转换等操作。
• 特别是证明了对于最近舍入（RN）方式，无论是进行舍入操作还是补码转换操作，只需要计算A+B和A+B+1就可以得到所有可能的结果。通常利用混合加法器（ComAdd）技术来完成同时计算 A+B 和 A+B+1 两个结果，通过共用内部硬件的方法同时计算A+B和A+B+1以减少总体规模。得到所有可能存在的结果之后，通过对浮点数的末尾几位进行分析并结合符号位，完成正确结果的选择。这种优化方法减少了一个有效加法操作。但其代价是必须修改两条路径上有效位的加法器，以产生 A+B 和 A+B+1 。
• 对于正、负无穷舍入，还需要计算 A+B+2 。因为当…。为了完成ｓｕｍ＋２运算，Quach与Flynn提出位于FAR路径的有效位加法器之上添加一排半加器。